|
Genauigkeit vormetrischer Längeneinheiten
Vormetrische Längeneinheiten lassen sich durch Rechnung aus der Nippur-Elle (Code A1) ableiten (Ableitung). Die Ableitung durch Rechnung ändert die Abweichung vom Sollwert, den prozentualen ‚Fehler', nicht, mit der die jeweils abgeleitete Maßeinheit behaftet ist. Dieser ‚Fehler' ist so groß wie derjenige, mit dem die Nippur-Elle bekannt ist.
Wenn man die Länge der Nippur-Elle von dem Exemplar herleiten würde, das im Museum in Istanbul liegt, würde man Fehler übernehmen, die bei der Eichung des Exemplars gemacht worden sind. Da ist nicht nur der Fehler, mit dem die Länge der Elle aufgetragen ist, sondern da sind auch noch die Fehler, mit denen die anderen Einheiten wie etwa der Fuß oder die palma abgetragen sind. Selbst wenn man diese Fehler mitteln würde, ergäbe das keine optimale Länge.
Die Projektgruppe 'Maße - Musik - Mathematik' MMM) im Arbeitskreis Archäometrie der Fachgruppe analytische Chemie in der Gesellschaft Deutscher Chemiker hat im Verlaufe vieler Jahre 872 Messskalen in Museen und in der Literatur gesammelt und identifiziert. Wenn man diese Skalen miteinander vergleichen will, muss man jeweils auf dieselbe Normlänge, etwa die Elle oder palma, besser aber den Fuß umrechnen, beispielsweise Ellen oder Doppelfuß in Fuß, und dann die unterschiedlichen Längen betrachten. Zweckmäßigerweise erstellt man dazu eine Häufigkeitsverteilungskurve ohne eine weitere Vorgabe als die, dass man die Fußlängen zu Klassen von 0,5 bis 0,3 mm Weite zusammenfasst. Diese Klassen werden so in eine Grafik eingetragen, dass man auf der Abszisse die Klassen, auf der Ordinate die Häufigkeit selbst, also die Stück (Anzahl) abträgt. So ergibt sich eine Gruppierung von vielen Treppenkurven. Jede einzelne Treppenkurve approximiert eine Gaußverteilungskurve. Die Maxima der vielen Gauß-Verteilungen fallen jeweils mit einer durch Rechnung erhaltenen Maßeinheit zusammen. Das ist der Beweis dafür, dass die rechnerischen Ableitungen richtig sind. Die durch die Gaußverteilung dargestellten Streuungen lassen sich als Variationskoeffizient beziffern. Der Variationskoeffizient ist die mit 100 multiplizierte und durch den Mittelwert der Verteilung dividierte Standardabweichung. (Zum Begriff der Standardabweichung vergl. evtl. Lexikon oder Lehrbuch der Statistik) Die beobachteten Variationskoeffizienten sind in der Regel kleiner als 0,2 %. Das bedeutet, dass die antiken/vormetrischen Längeneinheiten mit einer Genauigkeit von besser als 0,2 % über die Jahrtausende und die Tausende von Kilometern transportiert worden sind. Für jede Maßeinheit ist die aufgefundene Genauigkeit etwas anders, aber meistens unter 0,2 % Abweichung. Dazu die Tabelle der Mittelwerte der aufgefundenen Maßeinheiten.
|
A1
|
Nippur-Elle
|
518,90 +/- 0,911 mm
|
VK = 0,176%
|
n =19
|
|
A2
|
Erdfuß
|
230,10 +/- 0,679 mm
|
VK = 0,295%
|
n =7
|
|
A3
|
Baumaß
|
287,30 +/- 0,563 mm
|
VK = 0,196%
|
n =4
|
|
A4
|
Salamis-Elle
|
483,50 +/- 2,083 mm
|
VK = 0,431%
|
n =7
|
|
|
|
|
|
|
|
B1
|
Ägyptische Königselle
|
523,95 +/- 0,875 mm
|
VK = 0,167%
|
n =48
|
|
B2
|
Große ägypt. Königselle
|
529,00 +/- 0,662 mm
|
VK = 0,131%
|
n =20
|
|
B3
|
Vitasti
|
271,70 +/- 1,280 mm
|
VK = 0,472%
|
n =3
|
|
|
|
|
|
|
|
C
|
pes Romanus
|
296,13 +/- 0,500 mm
|
VK = 0,169%
|
n =58
|
|
|
|
|
|
|
|
D
|
Gudea-Fuß
|
265,10 +/- 0,576 mm
|
VK = 0,217%
|
n =7
|
|
|
|
|
|
|
|
E1
|
Große Ptolemäische Elle
|
533,30 +/- 0,725 mm
|
VK = 0,136%
|
n =29
|
|
E2
|
Großer Ptolemäischer Fuß
|
354,68 +/- 0,977 mm
|
VK = 0,276%
|
n =3
|
|
E3
|
Oskisch-umbrischer Fuß
|
275,70 +/- 0,412 mm
|
VK = 0,149%
|
n =4
|
|
|
|
|
|
|
|
F1
|
Punischer Fuß
|
94,02 +/- 0,400 mm
|
2VK = 0,136%
|
n =46
|
|
F2
|
„Kompromiß"-Fuß
|
297,83 +/- 0,270 mm
|
VK = 0,091%
|
n =12
|
|
F3
|
Vindonissa-Fuß
|
292,38 +/- 0,470 mm
|
VK = 0,161%
|
n =30
|
|
|
|
|
|
|
|
G
|
pes Drusianus
|
333,40 +/- 0,163 mm
|
VK = 0,049%
|
n =3
|
|
|
|
|
|
|
|
H1
|
Attisch-olympischer Fuß
|
310,60 +/- 0,388 mm
|
VK = 0,125%
|
n =14
|
|
H2
|
„Äginetischer" Fuß
|
314,00 +/- 0,432 mm
|
VK = 0,138%
|
n =9
|
|
|
|
|
|
|
|
I1
|
Pied du Roi
|
324,20 +/- 0,811 mm
|
VK = 0,250%
|
n =8
|
|
I2
|
Samisch-ionischer Fuß
|
347,70 +/- 0,597 mm
|
VK = 0,172%
|
n =7
|
|
I3
|
Kleiner Ptolemäischer Fuß
|
308,57 +/- 0,500 mm
|
VK = 0,162%
|
n =13
|
|
I4
|
Milesischer Fuß
|
317,00 +/- 0,301 mm
|
VK = 0,095%
|
n =9
|
|
|
|
|
|
|
|
J1
|
„Neue" Elle/gemeingr. Fuß
|
316,10 +/- 0,323 mm
|
VK = 0,102%
|
n =11
|
|
J2
|
Maß von Abydos
|
319,30 +/- 0,125 mm
|
VK = 0,039%
|
n =3
|
|
J3
|
Byzantinischer Fuß
|
321,30 +/- 0,205 mm
|
VK = 0,064%
|
n =3
|
|
|
|
|
|
|
|
N1
|
?-Elle (Ägypten)
|
536,70 +/- 0,572 mm
|
VK = 0,106%
|
n =3
|
|
|
|
|
|
|
|
P
|
Pythischer Fuß
|
248,4
|
|
n =1
|
|
Da sich die einzelnen vormetrischen Längeneinheiten durch Rechnung aus der Nippur-Elle herleiten lassen, kann man von einer aufgefundenen und identifizierten Skala ausgehend sozusagen 'rückwärts', d.h. entgegen dem Verlauf ihrer Entstehungsgeschichte, die Länge der Nippur-Elle wieder errechnen. Beispielsweise kann man aus 50 Exemplaren des Römischen Fußes (Code C) durch Division mit 16 und Multiplikation mit 28 unmittelbar die Länge der Nippur-Elle erhalten.
Die so erhaltenen einzelnen Werte streuen um den Mittelwert in dem Maße, wie die aufgefundene Skala jeweils vom Bestwert entfernt ist. Aus dieser Gaußverteilung lassen sich wieder Mittelwert, Standardabweichung und Variationskoeffizient (VK) berechnen (Wissenschaftlicher Taschenrechner)
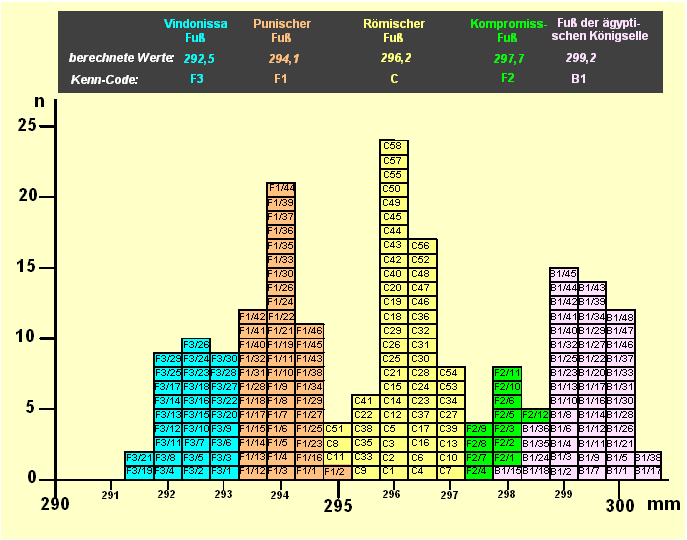 zum Vergrößern klicken Sie bitte auf die Abbildung zum Vergrößern klicken Sie bitte auf die Abbildung
Aus den insgesamt gesammelten Maßskalen ergaben sich seinerzeit 440 Werte für die Nippur-Elle. Der Mittelwert dieser 440 Werte liegt bei 518,30 mm/Elle, der Variationskoeffizient der daraus erhältlichen Gaußkurve bei 0,168 %. Das ist die Genauigkeit, mit der bis zur Einführung des Meters die alten Maße tradiert wurden.
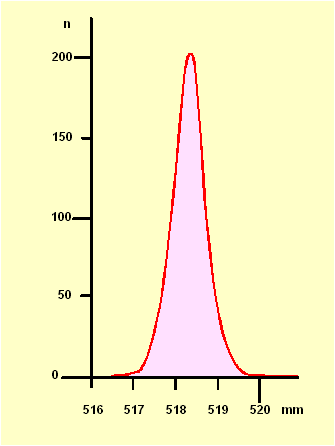 |
Je mehr Exemplare aufgespürt werden können, desto sicherer und genauer liegt der Wert der (berechneten) Nippur-Elle fest: Der Vertrauensbereich engt sich zunehmend ein. Der Vertrauensbereich ist die Strecke, in der die genaue Länge der Nippur-Elle mit einer vorgegebenen Sicherheit (beispielsweise 95 %) gelegen hat. Er ist umgekehrt proportional der Wurzel der Anzahl der eingehenden Maßskalen. Bei den betrachteten 440 Skalen liegt der Vertrauensbereich bei +/- 0,042 mm. Dadurch, dass die Zahl der aufgefundenen Skalen sich auf über 872 mehr als verdoppelt hat, wurde diese Streuung nicht halbiert, sondern nur um 1/√2 verbessert. Der Vertrauensbereich ist also auf ca. +/- 0,04 % gesunken d.h. verbessert.
Das bedeutet, dass die Nippur-Elle so genau festliegt, dass erst die fünfte Stelle die unsichere ist. Dieser Wert ist eine reine Rechengröße. Es hat nie einen realen Maßstab mit dieser Genauigkeit gegeben. Er darf nur deshalb berechnet werden, weil a) die historische Entwicklung der vormetrischen Maßeinheiten abgeschlossen und b) der Englische Fuß ganz genau an das Meter gebunden ist, das ungleich genauer festliegt. Für die Praxis bedeutet das, dass es genügt, alle vormetrischen Längenmaße mit vier zählenden Stellen ohne eine +/- Angabe zu verwenden.
Es darf nicht vergessen werden, dass die Angabe, die Nippur-Elle sei 518,30 mm lang, genau genommen einen Proportionalitätsfaktor darstellt. Es sind richtig ausgedrückt 518,30 mm/Elle. Man kann zwar - und muss es bei metrologischen Untersuchungen - den digitus auf 4 Stellen genau angeben, aber kein Mensch der Antike war in der Lage, einen digitus so genau auszumessen. Vernachlässigt man aber die dritte oder vierte Stelle, dann kommt es bei der Multiplikation mit Zahlen der Art, dass der 10-Meter-Bereich erreicht wird, zu unerträglichen Fehlern.
Weil alle Maßeinheiten rechnerisch auf die Nippur-Elle zurückgeführt werden können und diese auf vier zählende Stellen genau festliegt, d.h. die fünfte ist die unsichere Stelle, können umgekehrt auch die anderen Maßeinheiten mit dieser Genauigkeit angegeben werden. Deshalb wird hier keine +/- Angabe gemacht. Es genügt, nur vier der hier angegebenen fünf Stellen zu benutzen.
|
Megalithisches Yard
|
Code MY
|
40 megal. inches
|
829,36 mm/Yard
|
|
|
|
|
|
|
Nippur-Elle
|
Code A1
|
30 digiti
|
518,35 mm/Elle
|
|
Erdfuß
|
Code A 2
|
10 unciae
|
230,38 mm/Fuß
|
|
Baumaß
|
Code A 3
|
16 digiti
|
287,97 mm/Fuß
|
|
Salamis-Elle
|
Code A 4
|
24 digiti
|
483,79 mm/Elle
|
|
|
|
|
|
|
Ägyptische Königselle
|
Code B 1
|
28 digiti
|
523,61 mm/Elle
|
|
Große Ägypt. Königselle
|
Code B 2
|
28 digiti
|
528,90 mm/Elle
|
|
Shaku
|
Code B 2
|
10 unciae
|
302,23 mm/Fuß
|
|
Vitasti
|
Code B 3
|
16 digiti
|
272,01 mm/Fuß
|
|
|
|
|
|
|
Röm. Fuß; pes monetalis
|
Code C
|
16 digiti
|
296,20 mm/Fuß
|
|
|
|
|
|
|
Gudea-Fuß real
|
Code D 1
|
16 digiti
|
264,6 mm/Fuß
|
|
Gudea-Fuß ideal
|
Code D 2
|
16 digiti
|
265,40 mm/Fuß
|
|
Philetärischer Fuß
|
Code D
|
20 digiti
|
331,25 mm/Fuß
|
|
|
|
|
|
|
Große Ptolemäische Elle
|
Code E 1
|
28 digiti
|
533,17 mm/Elle
|
|
Großer Ptolemäischer Fuß
|
Code E 2
|
16 digiti
|
355,45 mm/Fuß
|
|
Oskisch-umbrischer Fuß
|
Code E 3
|
16 digiti
|
275,63 mm/Fuß
|
|
|
|
|
|
|
Punischer Fuß
|
Code F 1
|
16 digiti
|
294,00 mm/Fuß
|
|
Kompromiß'-Fuß’
|
Code F 2
|
16 digiti
|
297,70 mm/Fuß
|
|
Vindonissa-Fuß
|
Code F 3
|
16 digiti
|
292,48 mm/Fuß
|
|
Drusian. /kret.-äginet. Fuß
|
Code G1
|
18 digiti
|
333,23 mm/Fuß
|
|
spätbyzantinischer Fuß
|
Code G2
|
16 digiti
|
312,38 mm/Fuß
|
|
|
|
|
|
|
Attisch-olympischer Fuß
|
Code H 1
|
16 digiti
|
311,01 mm/Fuß
|
|
'Äginetischer' Fuß
|
Code H 2
|
16 digiti
|
314,16 mm/Fuß
|
|
|
|
|
|
|
Pied de Roi
|
Code I 1
|
16 digiti
|
323,82 mm/Fuß
|
|
Samisch-ionischer Fuß
|
Code I 2
|
16 digiti
|
347,32 mm/Fuß
|
|
Kleiner Ptolemäischer Fuß
|
Code I 3
|
16 digiti
|
308,48 mm/Fuß
|
|
Milesischer Fuß
|
Code I 4
|
16 digiti
|
317,35 mm/Fuß
|
|
|
|
|
|
|
'Neue' Elle
|
Code J 1
|
28 digiti
|
526,79 mm/Fuß
|
|
Gemeingriechischer Fuß
|
Code J 1
|
16 digiti
|
316,08 mm/Fuß
|
|
Maß von Abydos
|
Code J 2
|
16 digiti
|
318,93 mm/Fuß
|
|
Byzantinischer Fuß
|
Code J 3
|
16 digiti
|
320,58 mm/Fuß
|
|
|
|
|
|
|
Indus-Fuß
|
Code K
|
16 digiti
|
345,57 mm/Fuß
|
|
|
|
|
|
|
Pythischer Fuß
|
Code P
|
16 digiti
|
248,81 mm/Fuß
|
|
|
|
|
|
|
Tschi ( China )
|
Code T
|
10 unciae
|
317,5 mm/Fuß
|
|
(Hier nicht aufgeführte Längeneinheiten wie der sogen. dorisch-phaidonische Fuß gibt es nicht. Der sogen. Benediktinische Werkschuh oder der sogen. Karolingische Fuß sind gleich dem Drusianischen Fuß, Code G1)
vorige Seite zum Inhaltsverzeichnis nächste Seite
|


