|
Ableitung der alten Längeneinheiten und deren rechnerisches Verhältnis
Vorbemerkungen
Weil in der Literatur gleiche Längeneinheiten zum Teil verschiedene Bezeichnungen haben und andererseits unterschiedliche Längeneinheiten dieselbe Bezeichnung, haben alle selbstständigen Maß-einheiten einen Code bekommen, mit dem sie eindeutig identifiziert werden können. So werden Verwechslungen und der Streit um den 'richtigen' Namen vermieden. Zugleich ist dokumentiert, dass nur die Länge, nicht der Name einer Längeneinheit das Charakteristische ist.
A. THOM entdeckte in den 60er Jahren des vorigen Jahrhunderts eine Längeneinheit an megalithischen Steinsetzungen, die er Megalithisches Yard, MY, nannte. Sie ist 829,05 +/- 0,91 mm lang. Später stellte W. RASCH fest, dass diese Einheit schon viel früher, nämlich bei bandkeramischen Hausgrundrissen, verwendet worden ist. Diese datieren generell vor 5000 v. Chr., teilweise noch vor 5500 v. Chr. (sogen. Radiokarbondaten und Dendrodaten). THOM und RASCH betonen, dass sie Befunde haben, die nahe legen zu vermuten, dass das MY geviertelt gewesen ist, also 829,4 mm : 4 = 207,35 mm als Grundeinheit angesehen werden könnte. Diese Länge ist offensichtlich eine Spanne (12-digiti-Länge) zur Nippur-Elle, denn 207,35 mm : 12 x 30 = 518,37 mm.
Weil sich historisch betrachtet alle Längenmaßeinheiten auseinander entwickelt haben, kann man alle vormetrischen Längenmaßeinheiten unter Beachtung ihrer Unterteilungen auseinander ableiten und so umrechnen, d.h. ihren Bildungsweg von der Urelle, der Nippur-Elle, Code A1, als Ableitung verfolgen oder aus einer speziellen Maßeinheit wie etwa dem pes Romanus, Code C, zurückverfolgen. Die antiken Maßeinheiten sind in diesem Sinne kohärent.
Das folgende Bild zeigt eine Übersicht:
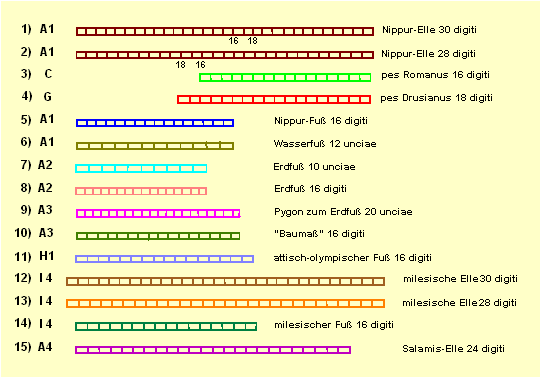
I 55 Weil die Nippur-Elle (Code A1) zu 518,30 mm 30 digiti hat, ist der digitus 518,30 : 30 = 17,277 mm lang. Macht man aus diesem digitus eine Elle zu nur 28 digiti, weil das besser zu einem Fuß von 16 digiti paßt (28 : 16 = 7 : 4), dann ist diese (neue) Elle 483,79 mm lang. Diese Ellenlänge wurde zuerst am metrologischen Relief von Salamis (I. DEKOULAKOU) entdeckt und heißt daher Salamis-Elle, Code A4.
Später wurde sie in Lepenski Vir, ehemaliges Jugoslawien, an Hausgrundrissen nachgewiesen, die um 6000 v. Chr. datieren. Diese durch 14C datierten Grundrisse sind die ältesten datierten Nachweise der Verwendung eines Maßes. Ungenau datierte Maße an Hausgruben im Orient sind vermutlich älter
.
II Es gibt noch einen anderen Weg, um von der Nippur-Elle (Code A1) mit ihren 30 digiti zu einer Elle von 28 digiti zu kommen. Um die Mitte des 3 Jts. spätestens wurde, besonders in Ägypten, ihre Länge von 518,35 mm einfach nur noch in 28 Teile (also digiti) geteilt, wodurch der digitus auf 18,513 mm anwuchs. Dadurch stieg auch die Länge des 16-digiti-Fußes, und zwar auf 296,20 mm an. Es ist der Jahrtausende später so genannte Römische Fuß, pes Romanus, 'attische' Fuß, pes monetalis, Code C. In klassisch-römischer Zeit war die zugehörige Elle als Handelselle auf 1,5 Fuß gesunken, also 444,3 mm lang.
III Die pygme ist ein Fuß von 18 digiti Länge. Wird die pygme aus dem digitus des pes Romanus gebildet, dann ist sie 18,513 mm x 18 = 333,22 mm lang. In der Antike war diese Länge als pes Drusianus, Code G, bekannt. (vgl. XXI)
IV Der zur Nippur-Elle gehörende Nippur-Fuß, Code A1, ist 276,45 mm lang. Zunächst in 16 digiti geteilt, wurde er in Mesopotamien auch in 12 Unzen geteilt. Die Unze ist folglich 276,45 mm : 12 = 23,037 mm lang. So unterteilt wanderte die Fußlänge nach Osten und gelangte nach China, wo sie Wasserfuß genannt wurde. Da aber von Indien beginnend weiter nach Osten zu an sich im dekadischen System gerechnet wurde, wozu das duodezimale System nicht passt, zog man in China von der Länge des Wasserfußes zwei Unzen ab und erhielt so den Erdfuß. Er ist 10 Unzen oder 230,37 mm lang und hat den Code A2.
V Wahrscheinlich durch den Seidenhandel, was aber z. Zt. nicht beweisbar ist, gelangte dieser kurze Erdfuß wieder nach Westen, vielleicht nach Ostrom oder Byzanz. Dort wurde der Erdfuß nach Landessitte in 16 Teile, d.h. digiti geteilt, wodurch der digitus auf 14,398 mm absank. Es gibt eine sowohl in China als auch in Europa zu beobachtende Tendenz, dass die verwendeten Längeneinheiten mit der Zeit zunahmen. Nicht die Einheit als solche wurde heraufgesetzt, vielmehr wurde die kürzere Einheit weniger, die längere immer häufiger benutzt. Weil nun der Erdfuß so kurz war, begann man, seine eigene Obereinheit zu 20 digiti, also die pygon, zu verwenden und als 'Fuß' zu betrachten:
14,398 mm x 20 = 287,96 mm/pygon.
Zunächst war man sich natürlich bewusst, dass dieser 'Fuß' 20 digiti hatte, aber in einer Umgebung, in der üblicherweise der Fuß in 12 Unzen geteilt wurde, also duodezimal und nicht dekadisch gerechnet wurde, setzte sich bald die Unterteilung in 12 Unzen oder gegebenenfalls in 16 digiti durch. Dadurch war das sogenannte Baumaß zu 287,96 mm entstanden, Code A3, das im mittelalterlichen Deutschland weit verbreitet war.
VI Die pygme ist ein Fuß von 18 digiti Länge. Wird eine pygme aus dem digitus der Nippur-Elle oder des Nippur-Fußes gebildet (Code A1) - er ist 17,278 mm lang - dann folgt:
17,278 mm x 18 = 311,00 mm/Fuß.
Diese Länge wurde von den Griechen nach ihrer Sitte in 16 Teile, digiti, geteilt, ohne auf die Herkunft zu achten. In dieser Unterteilung begegnet uns dieser Fuß als attisch-olympischer Fuß, Code H1.
VII Zwar wurde zur Zeit des römischen Imperiums die Elle nur zu 1,5 Fuß gerechnet, aber das war eine 'späte' Entwicklung. Über 1000 Jahre vorher hat man aus dem 18,513 mm langen digitus des später so genannten pes Romanus eine Elle zu 30 digiti gebildet, wobei man offensichtlich auf alte Traditionen zurückgegriffen hat:18,513 mm x 30 = 555,39 mm/Elle.
In anderer kultureller Umgebung indes teilte man diese Elle wieder in 28 Teile, digiti, von 19,835 mm Länge. Hieraus ergibt sich ein Fuß von
19,835 mm x 16 = 317,37 mm/Fuß.
Es ist der Milesische Fuß, Code I 4, der besonders in Kleinasien sehr verbreitet war (Grab des Kyros!)
VIII Im Ägypten der I. Dynastie war die Nippur-Elle statt in 30 nur noch in 28 digiti unterteilt worden. Diese Teilung in 28 Teile blieb bis zum Untergang des ägyptischen Reiches für die verschiedenen Königsellen bestehen, im Gegensatz zu den Handelsellen mit 24 digiti = 1,5 Fuß. - Nach den Frühjahrshochwassern des Nils musste von den Marken an den nicht überschwemmten Uferrändern ausgehend das wieder fruchtbar gewordene Ackerland vermessen und den Eigentümern zugewiesen werden. Dabei trat das Problem der Halbierung der Fläche eines Quadrats auf. Ein Quadrat halbiert man, indem man die Diagonale halbiert und aus dieser Länge ein neues Quadrat bildet. Dadurch ist man un-ausweichlich auf die Diagonale verwiesen. Die Diagonale eines Quadrates mit einer glatten Zahl als Seitenlänge ergibt eine irrationale Zahl. Beispielsweise ist die Diagonale eines Quadrats mit der Seitenlänge 'eins' gleich 'Wurzel zwei'. Das konnte man im alten Ägypten zwar nicht rechnen, wohl aber zeichnen. Bei einem Quadrat mit der Seitenlänge einer pygon, also 5 palmae, ergibt sich nach Pythagoras 5² + 5² = 25 + 25 = 50.
Aus 50 wäre also die Quadratwurzel zu ziehen. Das geht aber so einfach nicht, wohl aber aus 49, was 7 ergibt. Die Diagonale ist 7 palmae - das passt ins ägyptische System - oder 28 digiti lang. Notwendigerweise ist aber dieser digitus zu groß: die Diagonale misst ja genau 7,07107 palmae, ist also rund 1 % länger. Ist die palma der 28-digiti-Nippur-Elle 4 x 18,513 = 74,052 mm lang, dann ist die neue palma 7,07107 x 74,052 mm : 7 = 74,804 mm lang. Der digitus ist ein Viertel davon : 18,701 mm, die Elle also 18,701 mm x 28 = 523,62 mm/Elle. Das ist die Ägyptische Königselle, Code B1.
IX In späteren Zeiten ist man nicht von der pygon der 28-digiti-Nippur-Elle ausgegangen, sondern hat die Quadratseite eine pygon der ägyptischen Königselle lang gemacht. Dadurch wurde die Diagonale noch einmal um rund 1 % länger: 7,07107 : 7 = 1,01015. Wenn man mit diesem Faktor die Königselle multipliziert: 1,01015 x 523,62 mm = 528,93 mm/Elle, so erhält man die Große Ägyptische Königselle, Code B2. Die Länge des Fußes zu dieser Elle ist 528,93 mm : 28 x 16 = 302,25 mm/Fuß. Diese Länge ist in Japan unter der Bezeichnung 'Shaku' bis zur Einführung des Meters in Gebrauch gewesen. Der Code ist selbstverständlich unverändert B2.
X Der Fuß zur Großen Ägyptischen Königselle, Code B2, ist 528,90 : 28 x 16 = 302,25 mm lang, wie soeben schon dargelegt, und wurde in Japan als 'Shaku' in 10 Teile (Unzen) geteilt. Multipliziert man diesen Wert mit 27/30, dann erhält man den in Persien bis zur Einführung des Meters verwendeten Vitasti und das Maß von Tiahuanako von gleicher Länge: 272,01 mm! Ausführlich geht die Rechnung so, dass zum Fuß die Elle von 528,90 mm gehört. Diese in 30 digiti geteilt und auf eine 27-digiti-Elle umgerechnet, ergibt dann 476,01 mm. Anderenorts folgt aus dieser Länge, als 28-digiti-Elle aufgefasst, ein 16-digiti-Fuß von 476,01 :28 x 16 = 272,01 mm, Code B3.
XI Gudea von Lagash, Zweistromland (ca. 2600 v. Chr.), war ein sehr mächtiger 'Gaufürst' (Enlil), der ein enormes Bauprogramm durchgeführt hat und von sich zahlreiche Statuen anfertigen ließ. Weil ihm die Unterteilung der Elle in 28 digiti und des Fußes in 16 digiti missfiel, wollte er wieder zum dekadischen System zurückkehren. Er ordnete daher an, dass die Obereinheit von 6 Fuß (zu 16 digiti = 96 digiti), gi (Rohr) genannt, zukünftig 100 digiti lang sein solle. Dadurch schrumpft der digitus bezogen auf die Nippur-Elle.
17,278 mm/dig x 16 x 6 = 1658,7 mm. 1658,7 mm : 100 = 16,587 mm/digitus
16,587 mm x 16 = 265,39 mm/ Fuß
Dies ist die rechnerisch korrekte Umrechnung, und deshalb heißt die Fuß-Länge 'Gudea-Fuß ideal'. (Code D2).
An sich wollte aber Gudea eine Fußlänge von 20 digiti haben, damit deren fünf auf die Obereinheit gehen sollten. Er hätte dann eine Staffelung der Art gehabt: 20 digiti ein Fuß; 30 digiti eine Elle, 100 digiti ein 'Rohr'. 20 digiti entsprechen ja der pygon, und die alte Elle hatte 30 digiti.
Die in der Metrologie Fachkundigen sagten aber dem Gudea, dass das Sekundenpendel in Babylon zwei Ellen messe. Wie genaue Studien zeigten, ist es 992,25 mm lang. Das berechnete Pendel zu 60 digiti wäre aber 995,22 mm lang gewesen, d.h. rund 3 mm zu lang. Daraus zog Gudea den Schluss, dass das alte Maß nicht korrekt überliefert worden sei und ordnete an, dass auf das Sekundenpendel zu Babylon zu korrigieren sei, denn nur so bliebe man in der Harmonie der Welt. Dadurch wurde die Elle zu 30 digiti nun 496,13 mm lang, der Fuß zu 20 digiti 330,75 mm lang, der digitus 16,538 mm lang und der Fuß zu 16 digiti 264,6 mm lang. Es ist der 'Gudea-Fuß real' mit dem Code D1. Auf einem Plan auf den Knien einer aus Diorit gefertigten Sitzstatue des Gudea, heute im Louvre, ist ein Fuß-Maß dieser Länge abgetragen.
Der 20-digiti-Fuß ist unter dem Namen 'Philetärischer Fuß' in die Geschichte der Metrologie eingegangen. Selbstverständlich hat auch dieser Fuß den Code D (D3). Es ist der einzige Fall in der Geschichte der Metrologie, wo ein Maß eine Streuung von mehr als 0,2 %, nämlich 0,3 % hat. Das bedeutet, dass man bei Untersuchungen von alten Bauwerken wegen der Fehlerstreuung nach Gauß nicht entscheiden kann, ob D1 oder D2 vorliegt. Andererseits haben sich sowohl aus D2 (außerhalb Mesopotamiens) als auch aus D1 im Verlauf der Geschichte Maßeinheiten hergeleitet. Da von diesen Maßeinheiten Exemplare vorliegen, kann man durch Ausmessen deren Länge genau bestimmen und so ihre Herkunft aus D1 oder D2 trennen.
Aus den vier Haupt-Untermaßeinheiten mit den Codes B1, C, D1 und D2, die ihrerseits direkt aus der Nippur-Elle, Code A1, hervorgegangen sind (wobei man inzwischen weiß, dass MY und A1 demselben System angehören), leiten sich ausnahmslos alle anderen vormetrischen Maßeinheiten ab.
Die Maßeinheiten mit den Haupt-Codes A, B, C und D sind bis hierhin abgehandelt.
vorige Seite zum Inhaltsverzeichnis Fortsetzung
|


